競技プログラミングでたまに出る「全方位木DP」を解説

はじめに

DPにはさまざまな名前がつくことがあります。区間DP、挿入DP、ビットDPなど。

全方位木DPというのもその中の一つです。私がこれをはじめて学んだ時、とても感動したのを覚えています。

問題として全方位木DPが題材となっている場合、素の実装力が高い人は2回のDFSを1から書いてしまう人もいるようですが、これは稀な例で、全方位木DPの抽象化と調べると、ちょうどセグ木のように頂点や辺で持つ値の型や計算方法を定義してあげるとあとはフレームワークに任せることが出来るようにした記事がいくつか出てきます。

私も、最初はそのうちの1つを実装して使いました。しかし、別の問題に出会った時にその抽象化があまりにも全方位木DPの動きを隠蔽しすぎていて柔軟性が足りないということに気づき、自分なりの抽象化と実装を模索しました。

今回はそれを紹介します。

全方位木DPとは

全方位木DPというのは、英語ではRerootingといいます。実際に英語名の方が動作についてよく表していて、全方位という表現はミスリーディングだと思います。

問題としては典型的にはこういうものです: 「各頂点を根とした時の各部分木のなんらかの値を計算せよ」

部分木の値を計算すれば、各頂点の値も、さらに辺の数x2回の計算を行えば計算出来ますから、部分木の値を計算するというのにとどめて計算量の観点では問題がありません。実際に、こちらの方が活用しやすいです。

一つの根からDFSをして木DPをすることを頂点数n回繰り返すのであれば、計算量はO(n^2)となります。従って、n=1000程度ならばそれでも間に合うのですが、全方位木DPの問題は典型的には、n=100000とか、二乗が不可能な制約をしてきます。この制約下では、許されるのはO(n)かO(nlogn)くらいです。

全方位木DPでは、計算の特殊性に着目して、計算を省略します。

1回目のDFSでは、通常の木DPを行い、 2回目のDFSでは、今の根の子を根に持ち上げるという操作（Rerooting）をO(1)で実行していき、トータルの計算量をO(n)にします。（つまり最終的には全頂点が根を経験することになります）

このためには当然、求める計算がRerooting可能であることが必要となります。そういった場合に、計算を省略していけるというのがポイントです。

アルゴリズム

アルゴリズムを説明します。少し抽象的な話で理解がしにくい場合は、今求めるものが部分木のサイズであるという具体例を考えるとわかりやすいと思います。

1回目のDFS

すでに述べたように1回目のDFSでは、通常の木DPを行います。

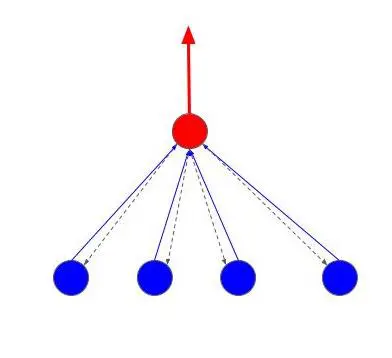
ある頂点からみた時の各部分木の値を、入辺の値と考えることにします。

すると、各頂点が入辺の値（青い辺）を使って、出辺の値（赤い辺）を計算することが出来ればよいことになります。そして、全方位木DPというのは、すべての有向辺についての値を計算することといえます。

2回目のDFS

2回目のDFSでは、1回目のDFSの根からスタートしてRerootingを再帰的に繰り返していきます。

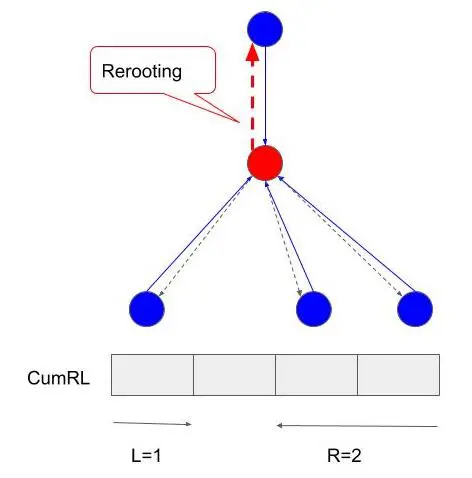
Rerootingをした時、図でいうと赤い点線で描いた辺の値を計算することになるのですが、子頂点分の計算量がかかってはO(n^2)になってしまいます。

そこでまず、累積和のようなものを左から右と右から左の両方向について計算します。この構造をCumRLと呼ぶことにしましょう。自分の子をRerootingする間はこのCumRLを使い回します。この際、持ち上げた子の部分を歯抜けにして、左L個と右R個という情報から値が計算出来る必要があります。これは足し算や掛け算では成り立ちますが、常に成り立つわけではないため、全方位木DPはこの特殊性を利用しているということがいえます。

こうすることで、CumRLの構築にO(n)、Rerootingの計算にO(n)ですから、トータルでO(n)の計算量となります。

疑似コードで書くとこんな感じになります。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def dfs_2nd(cur_root, par):
  chdp = []
  for ch in g.children(cur_root, par):
    chdp.push(dp[ch][cur_root])
  n = len(chdp)
  cumrl = CumRL(chdp)
  for i in 0..n:
    ch = g[cur_root][i]
    L = i
    R = n-(i+1)
    dp[cur_root][ch] = calc_dp(&cumrl, L, R)
  for ch in g.children(cur_root, par):
    dfs_2nd(ch, cur_root)

フレームワークの抽象化

全方位木DPの辺の値は、どのような性質を持つべきか考えます。

この型をTとすると、Tについて

id() -> T
fold(T, T) -> T

がCumRLを計算するために必要とわかります。

また、Rerooting時の計算として、

rerooting(&CumRL, Int, Int) -> T

のようなものが計算出来ればよいです。 1回目のDFSでもこの関数を使って出辺の値を計算していくことにします。

あとは、初期値として頂点や辺に何かしらの値を持たせることも許すとして、

rerooting(NVAL, EVAL, &CumRL, Int, Int) -> T

などと拡張すればほとんどの問題では十分に対応出来ます。

ご自由にどうぞ: rust-comp-snippets